大学物理III-9光的衍射
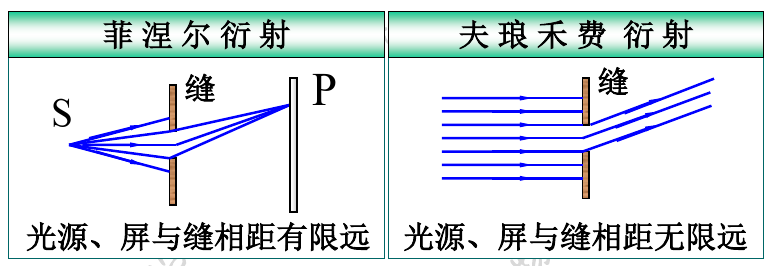
两种衍射模型——菲涅尔衍射和夫琅禾费衍射
半波带法
尝试找到一组波阵面的分割使两个半波带之间总存在一对对应点使其子波光线均为 $\dfrac{\lambda}{2}$ , 该组波阵面相遇叠加的结果为干涉相消

总结为如下情况
\[\begin{aligned} & a\sin \theta = 0 \quad & \text{中央明纹中心} \\ & a\sin \theta = \pm 2k\frac{\lambda}{2} \quad & \text{干涉相消} \\ & a\sin \theta = \pm 2(k+1)\frac{\lambda}{2} \quad & \text{干涉加强} \\ & a\sin \theta \neq k\frac{\lambda}{2} \quad & \text{介于明暗之间} \end{aligned}\]作近似 $\sin \theta \approx \tan \theta \approx \theta, \, \tan \theta = \dfrac{x}{f}$
得
(1) 第一暗纹的衍射角
半角宽度:
\[\theta_1 = \frac{\lambda}{a}\]第 $k$ 暗纹距中心的距离
\[x_k = \theta_k f = \frac{k\lambda}{a} f\]中央明纹宽度
\[\Delta x_0 = 2x_1 = 2f\frac{\lambda}{a}\]除了中央条纹外的其他条纹宽度
\[\Delta x = \theta_{k+1}f-\theta_{k}f = \frac{\lambda f}{a}\]单缝衍射的动态变化
单缝上下移动,根据透镜成像原理衍射图不变
圆孔衍射
中心亮圆(艾里斑)直径设为 $d$
\[\theta = \frac{d/2}{f} = 1.22 \frac{\lambda}{D}\]光学仪器的分辨本领
最小分辨角
\[\theta_0 = 1.22 \frac{\lambda}{D}\]光学仪器分辨率
\[\frac{1}{\theta_0} = \frac{D}{1.22\lambda} \propto D\]上式说明光学仪器的通光孔径 $D$ 越大,那么其分辨能力越强
光栅衍射
定义: 光栅常数
\[d = a + b\]其中 $a$ 为透光部分的宽度, $b$ 为不透光部分的宽度
数量级 $10^{-5} \text{\textasciitilde} 10^{-6} \mathrm{m} $
光栅的多缝干涉
相邻两缝的光程差
\[\delta = (a+b)\sin \theta\]光栅方程
\[d\sin\theta = \pm k\lambda, \, k=0,1,2,\ldots\]满足该方程的位置的条纹称为光栅的主极大
当光栅有 $N$ 条狭缝,那么有以下推论
(1) 相邻两主极大明纹之间有 $N-1$ 条暗纹
(2) 相邻两主极大明纹之间有 $N-2$ 条次级明纹
缺级现象
在某些方向上同时满足光栅方程的主极大条件和单缝衍射的暗纹条件,则该方向上的明纹将不会出现,这就是缺级现象
联立
\[\begin{cases} (a+b)\sin \theta = \pm k\lambda,\, & k=0,1,2,3,\ldots \\ a\sin\theta = \pm k^\prime\lambda,\, & k^\prime=1,2,3,\ldots \end{cases}\]得到缺级公式
\[k = k^\prime \frac{a+b}{a}\]求屏上可观察到的级次
由 $\theta \lt \dfrac{\pi}{2}$ 可得
\[k_{\text{max}} \lt \frac{a+b}{\lambda}\]