大学物理III-8光的干涉

由近似 $ \sin \theta = \tan \theta = x / D $ 得波程差
\[\Delta r = r_2 - r_1 \approx d\sin \theta = d \frac{x}{D}\]某位置条纹的明暗条件
\[\Delta r = \frac{d}{D}x = \begin{cases} \pm k\lambda & \text{加强} \\ \pm (2k+1)\dfrac{\lambda}{2} & \text{减弱} \end{cases} k = 0,1,2,\ldots\]特取相邻两条纹,易推得条纹间距
\[\Delta x = \frac{D\lambda}{d}\]由于中央条纹(0级, $k=0$ )为明条纹,因此亮条纹位置也便于记忆:
\[x = \pm k \frac{D}{d}\lambda\]半波损失
光从光速较大的介质射向光速较小的介质时,反射光的相位相较入射光的相位变化 $\pi$
即反射光和入射光之间附加了半个波长的的波程,附加波程差取 $\pm \frac{\lambda}{2}$ 均可
光程
\[L=nd\] \[\Delta \varphi = \frac{2\pi}{\lambda} L\]光在折射率为 $n$ 的介质中通过 $d$ 的几何路径时的相位改变与光在真空中通过 $nd$ 的几何路径时的相位改变相同
增透和增反
等倾干涉

光程差
由于几何和介质不同而产生的部分:
\[\delta_1 = n_2(\overline{AC} + \overline{BC}) - n_1\overline{AD}\]半波损失所贡献的部分:
\[\delta_2 = \begin{cases} 0 & n_1 \lt n_2 \lt n_3 \text{或} n_1 \gt n_2 \gt n_3 \\ \dfrac{\lambda}{2} & n_1 \lt n_2 \gt n_3 \text{或} n_1 \gt n_2 \lt n_3 \end{cases}\] \[\delta = \delta_1 + \delta_2\]等倾干涉实验
点光源照明
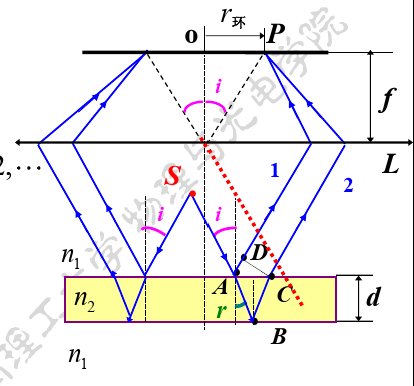
光程差是入射角的函数,即 $\delta = 2d\sqrt{n_2^2 - n_1^2\sin^2 i} + \dfrac{\lambda}{2} = \delta(i)$
于是倾角相同的光线都对应到同一条干涉条纹上
条纹特点:
\[r_{\text{环}} = f\tan i\]面光源照明
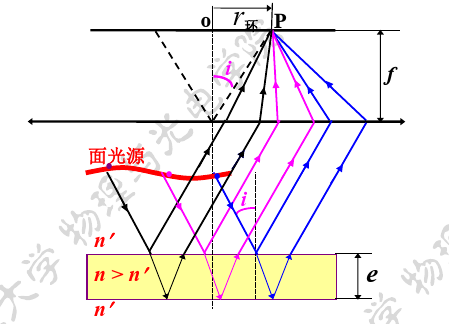
只要入射角相同都将汇聚在同一个干涉环上(非相干)
等厚干涉
光入射到厚度不均匀的透明介质薄膜上,当入射角保持不变的时候光程差仅与膜的厚度有关,凡厚度相同的地方光程差相同,从而对应同一条干涉条纹
\[\delta = 2d\sqrt{n_2^2-n_1^2\sin^2 i} + \frac{\lambda}{2} = \begin{cases} k\lambda & \text{亮纹} \\ (2k+1)\dfrac{\lambda}{2} & \text{暗纹} \end{cases} \, k = 0,1,2,3,\ldots\]劈尖干涉

夹角很小的介质薄片或薄膜
当光垂直入射时 $\sin i = 0$
\[\delta = 2nd + \frac{\lambda}{2} = \begin{cases} k\lambda \, & \text{亮纹} \, k=1,2,3,\ldots \\ (2k+1)\dfrac{\lambda}{2} \, & \text{暗纹} \, k=0,1,2,\ldots \end{cases}\]在棱边处 $d=0$ 由于半波损失而形成暗纹
相邻明纹厚度差
\[l \alpha \approx l\sin \alpha = \Delta d = d_{k+1}-d_k = \frac{\lambda}{2n}\]检查光学元件表面质量

深度
\[H = \frac{a}{b} \cdot \frac{\lambda}{2}\]牛顿环
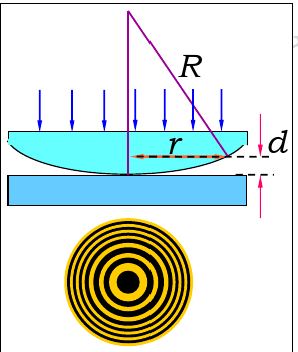
光程差在空气中产生:
\[\delta = 2d + \frac{\lambda}{2} = \begin{cases} k\lambda \, (k=1,2,\ldots) \quad & \text{明环}\\ (2k+1)\dfrac{\lambda}{2} \, (k=0,1,\ldots) \quad & \text{暗环} \end{cases}\]由 $ r^2 = R^2 - (R-d)^2 = 2dR - d^2, \, R d^2 \approx 0 $ 得
\[r = \sqrt{2dR} = \sqrt{(\delta - \frac{\lambda}{2})R}\]即
明环满足:
\[r^2 = R \cdot (k\lambda - \frac{\lambda}{2})\]暗环满足:
\[r^2 = R \cdot k\lambda\]于是相邻明/暗环又有
\[r_{k+m}^2-r_k^2=mR\lambda \tag{*}\]检验平凸透镜曲率半径是否合格

由 $(*)$ 得曲率半径
\[R = \frac{r_{k+m}^2-r_k^2}{m\lambda}\]